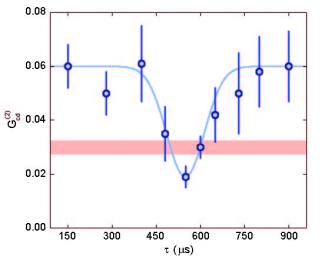
Observation of entanglement in a cold atom analog of cosmological preheating
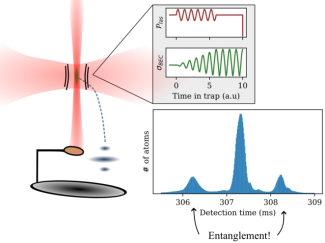
We observe entanglement between collective excitations of a Bose-Einstein condensate in a configuration analogous to particle production during the preheating phase of the early universe. In our setup, the oscillation of the inflaton field is mimicked by the transverse breathing mode of a cigar-shaped condensate, which parametrically excites longitudinal quasiparticles with opposite momenta. After a short modulation period, we observe entanglement of these pairs which demonstrates that vacuum fluctuations seeded the parametric growth, confirming the quantum origin of the excitations. As the system continues to evolve, we observe a decrease in correlations and a disappearance of non-classical features, pointing towards future experimental probes of the less understood interaction-dominated regime.
Under review but available on ArXiv.
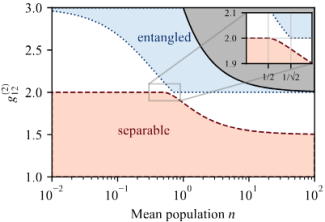
Quantifying two-mode entanglement of bosonic Gaussian states from their full counting statistics
We study the entanglement properties of two-mode bosonic Gaussian states from their multi-mode counting statistics. We introduce the idea that measuring high-order correlations of particle numbers can reveal entanglement without making any assumptions about the coherence of the fields. In particular, we show that the two- and four-body number correlations are sufficient to fully characterize the entanglement of two-mode bosonic Gaussian states for which each mode exhibits a thermal distribution. In addition, we derive an entanglement witness based on two-body correlations alone. Our findings are of great importance because it becomes possible to reveal entanglement in a series of recent experiments.
Under review but available on ArXiv.
Coherent coupling of momentum states: selectivity and phase control
We demonstrate the effect of pulse shaping in momentum selective atomic Bragg diffraction. We compare temporal square pulses, which produce sidelobes in momentum space, with other shapes which can produce more nearly square momentum distributions. We produce pulses that simultaneously address two sets of velocity classes (Alice and Bob on the left) and demonstrate that we can control the differential phase imprinted on them in a way that is insensitive to laser phase fluctuations.
Leprince et al. Coherent coupling of momentum states: Selectivity and phase control. Phys. Rev. A 111, 063304 (2025)
Sub-shot-noise interferometry with two-mode quantum states
We study the feasibility of sub-shot-noise interferometry with imperfect detectors, starting from twin Fock states and two-mode squeezed vacuum states. We derive analytical expressions for the corresponding phase uncertainty. We find that one can achieve phase shift measurements below the standard quantum limit, as long as the losses are smaller than a given threshold, and that the measured phase is close enough to an optimal value. We provide our analytical formulas in a python package, accessible online.
Marolleau et al. Sub-shot-noise interferometry with two-mode quantum states. Phys. Rev. A 109,023701 (2024)
Thermal counting statistics in an atomic two-mode squeezed vacuum state
We measure the population distribution in one of the atomic twin beams generated by four-wave mixing in an optical lattice. Although the produced two-mode squeezed vacuum state is pure, each individual mode is described as a statistical mixture. We confirm the prediction that the particle number follows an exponential distribution when only one spatio-temporal mode is selected. We also show that this distribution accounts well for the contrast of an atomic Hong-Ou-Mandel experiment. These experiments constitute an important validation of our twin beam source in view of a future test of a Bell inequality.
Perrier et al. Thermal counting statistics in an atomic two-mode squeezed vacuum state. SciPost 7, 002 (2019)
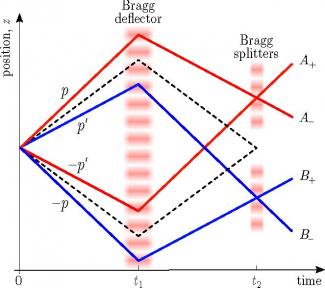
Two-Particle Four-Mode Interferometer for Atoms
We have used a variant of the Hong Ou Mandel setup described below to realize a two-particle interferometer with four input and four output ports as shown in the figure. The source generates atom pairs in a superposition of different momentum states: |ψ) ~ |p,-p) + |p',-p'). When such a state is injected into the atom interferometer, the probability of detecting an atom at each output port is 1/4, independent of any interferometer phase. The correlations between the different output ports however do vary as a function of the relative phase of the two closed circuits (red and blue in the figure). We have demonstrated this effect in our apparatus. An improved version of this experiment can lead to the violation of a Bell inequality involving the motional degrees of freedom of freely falling massive particles.
Dussarrat, P. et al. Two-Particle Four-Mode Interferometer for Atoms. Phys. Rev. Lett. 119, 173202 (2017).
Atomic Hong-Ou-Mandel effect
The Hong Ou Mandel (HOM) effect is a remarkable illustration of 2 particle interference. Two identical particles arrive at the input ports of a beam splitter. If they are perfectly overlapped, they never exit in opposite output ports. The effect is well known for photons. We have recently performed the analogous experiment for atoms.
Lopes, R. et al. Atomic Hong–Ou–Mandel experiment. Nature 520, 66–68 (2015).
Second-order coherence of superradiance from a Bose-Einstein condensate
A BEC has sufficient optical thickness to act as a gain medium. When an elongated BEC is excited by a laser beam, the gain causes the spontaneous emission to be preferentially directed in the elongated direction, in so called endfire modes. Since it involves considerable gain and is highly directional, this emission resembles laser emission. We have measured the intensity (2nd order) correlation function of this emission and found that its statistical properties resemble those of a thermal source rather than those of a laser. We do this by observing the recoil of each atom undergoing a superradiant scattering process. Our detector allows us to construct the 2-atom correlation function and thereby infer the correlation function of the emitted light.
Lopes, R. et al. Second-order coherence of superradiance from a Bose-Einstein condensate. Phys. Rev. A 90, 013615 (2014).