Travaux théoriques
Nous menons des études théoriques sur la caractérisation et l’optimisation de la précision des mesures polarimétriques obtenues avec différentes architectures d’imageurs. Cela nous permet en particulier de définir les limites fondamentales de ces instruments en termes de précision.
Comment optimiser l'estimation du vecteur de Stokes ?
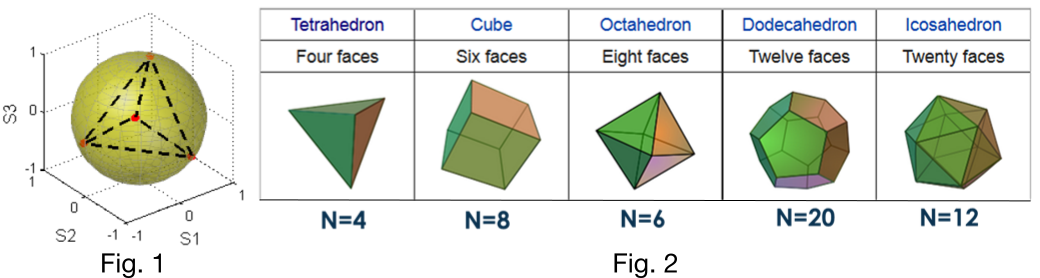
L’état de polarisation de la lumière est représenté par son vecteur de Stokes. Un polarimètre mesure ce vecteur en projetant la lumière sur un nombre N d’analyseurs de polarisation définis par leur vecteur de Stokes (N doit être supérieur ou égal à 4). Ces vecteurs peuvent être représentés comme des points sur la sphère de Poincaré (Fig 1). Dans la pratique, il est essentiel de déterminer les architectures de polarimètres qui donnent la meilleure précision d’estimation en présence de bruit de mesure. Il a été montré qu’en présence de bruit additif, les polarimètres optimaux sont définis par un ensemble de points sur la sphère de Poincaré formant un « spherical 2 design » [1,2]. Pour N=4 mesures, c’est un tétraèdre régulier (Fig. 1). Lorsque N est supérieur, il existe de nombreuses combinaisons permettant d’atteindre l’optimum. Parmi elles, on trouve les « solides platoniques » (Fig. 2).
Les contributions de notre équipe dans ce domaine sont les suivantes :
- Nous avons montré qu’en présence de bruit de Poisson (qui est la source de bruit dominante dans la plupart des applications d’imagerie), les architectures qui optimisent la précision sont également des « spherical designs » [3,4].
- Nous avons déterminé les architectures optimales pour la mesure de matrices de Mueller en présence de bruit additif et de bruit de Poisson : les états d’illumination et d’analyse doivent également former des « spherical designs » [5,6].
- C’est souvent l’estimateur pseudo-inverse qui est utilisé pour estimer le vecteur de Stokes. Cet estimateur est optimal en présence de bruit additif, mais pas en présence de bruit de Poisson. Cependant, nous avons montré que même dans ce cas, si l’architecture utilisée est un « spherical design », l’estimateur pseudo-inverse donne des résultats proches de l’estimateur du maximum de vraisemblance. L’estimateur pseudo-inverse, qui présente l’avantage d’être rapide à calculer, est donc une bonne alternative dans tous les cas [7].
Comment optimiser l'estimation des paramètres polarimétriques ?
Souvent, ce n’est pas le vecteur de Stokes qui est utilisé dans la pratique, mais des paramètres polarimétriques tels que le degré de polarisation (DOP), l’angle de polarisation (AOP) et l’ellipticité (EOP). Ces paramètres sont calculés à partir du vecteur de Stokes, mais la relation entre les deux est non-linéaire.
- Nous avons déterminé des approximations efficaces de la variance d’estimation de ces paramètres sous forme analytique dans le cas où le polarimètre a une structure de « spherical design » [8] et dans le cas où il est quelconque [9]. Ce dernier résultat permet de comparer la précision de deux architectures, même si elles ne sont pas optimales.
- Nous avons caractérisé le domaine de validité de ces approximations, et proposé des approximations plus complexes mais encore plus fidèles [10].
Comment simplifier les imageurs polarimétriques ?
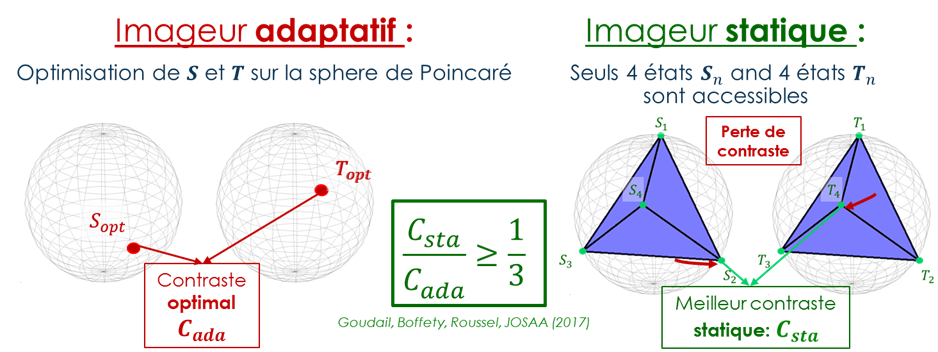
L’optimisation du contraste dans les imageurs polarimétriques nécessite des modulateurs totalement adaptatifs, qui sont complexes à mettre en œuvre et à calibrer. Pour des raisons pratiques, il est parfois préférable d’utiliser des polarimètres n’ayant que quelques états accessibles. Cela entraîne une perte de contraste, que nous avons quantifiée et dont nous avons montré qu’elle reste modérée dans tous les cas. Les imageurs polarimétriques statiques sont donc de bonnes alternatives aux systèmes totalement adaptatifs si une précision ultime n’est pas nécessaire [11,12].
Quelles sont les limites fondamentales du contraste en imagerie polarimétrique ?
Nous avons étudié de manière théorique et quantitative le gain apporté par un imageur polarimérique en termes de contraste par rapport à un imageur classique [13]. Cela nous a permis de mettre en évidence et comparer les limites fondamentales de plusieurs architectures d’imageur (voir figure ci-dessous) en présence de différents types de bruit (additif, Poisson, speckle) [14,15].
Références
[1] M. R. Foreman, A. Favaro, and A. Aiello, “Optimal frames for polarization state reconstruction,” Phys. Rev. Lett. 115(26), 263901 (2015).
[2] M. Foreman, F. Goudail, “On the equivalence of optimization metrics in Stokes polarimetry,” Opt. Eng. 58, 082410 (2019).
[3] F. Goudail, "Noise minimization and equalization for Stokes polarimeters in the presence of signal-dependent Poisson shot noise", Opt. Lett., 34(5), 647-649 (2009).
[4] F. Goudail, "Equalized estimation of Stokes parameters in the presence of Poisson noise for any number of polarization analysis states," Opt. Lett. 41, 5772-5775 (2016)
[5] G. Anna and F. Goudail, “Optimal Mueller matrix estimation in the presence of Poisson shot noise”, Opt. Express, 20 (19), 21331-21340 (2012).
[6] F. Goudail, "Optimal Mueller matrix estimation in the presence of additive and Poisson noise for any number of illumination and analysis states," Opt. Lett. 42, 2153-2156 (2017).
[7] F. Goudail, "Performance comparison of pseudo-inverse and maximum-likelihood estimators of Stokes parameters in the presence of Poisson noise for spherical design-based measurement structures," Opt. Lett. 42, 1899-1902 (2017).
[8] J. Dai, F. Goudail, M. Boffety, J. Gao, “Estimation precision of full polarimetric parameters in the presence of additive and Poisson noise,” Opt. Express 26, 34081-34093 (2018).
[9] J. Dai, F. Goudail, “Precision analysis of arbitrary full-Stokes polarimeters in the presence of additive and Poisson noise,” J. Opt. Soc. Am. A 36(7), 1229-1240 (2019).
[10] J. Dai, F. Goudail, “On the validity domain of approximations to estimation variance of polarization degree, azimuth and ellipticity,” J. Opt. Soc. Am. A 36(8), 1295-1305 (2019) (2019).
[11] F. Goudail, M. Boffety, “Performance comparison of fully adaptive and static passive polarimetric imagers in the presence of intensity and polarization contrast”, J. Opt. Soc. Am. A 33(9),1880-1886 (2016).
[12] F. Goudail, M. Boffety, S. Roussel, "Optimal configuration of static Mueller imagers for target detection," J. Opt. Soc. Am. A 34, 1054-1062 (2017).
[13] F. Goudail, J. S. Tyo, “When is polarimetric imaging preferable to intensity imaging for target detection ?”, J. Opt. Soc. Am. A 28 (1), 46-53 (2011).
[14] F. Goudail, M. Boffety, "Fundamental limits of target detection performance in passive polarization imaging," J. Opt. Soc. Am. A. 34, 506-512 (2017).
[15] J. Dupont, M. Boffety, F. Goudail, “Precision of polarimetric orthogonal state contrast estimation in coherent images corrupted by speckle, Poisson and additive noise,” J. Opt. Soc. Am. A 35, 977-984 (2018).