Thermoplasmonique
Équipe Thermoplasmonique
Son activité est principalement consacrée à l'étude des mécanismes de transport de la chaleur par rayonnement en champ proche. Il s’agit d’une part d’étudier les mécanismes fondamentaux qui régissent les échanges de chaleur et d’autre part de concevoir des matériaux fonctionnalisés pour la conversion d’énergie (conversion thermophotovoltaïque), le stockage d’information (nanophotolitographie) en passant par le management thermique à nanoéchelle, la détection infrarouge et la spectroscopie IR.
Membres
L’équipe thermoplasmonique est constitué de deux chercheurs permanents
Philippe Ben-Abdallah (Directeur de recherche CNRS)
Riccardo Messina (Chargé de recherche CNRS)
ainsi que d’un postdoctorant (Florian Herz).
Préambule
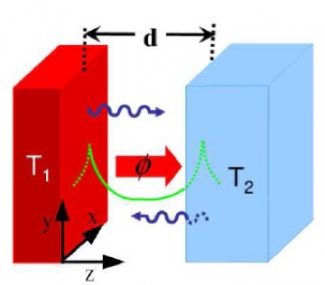
Lorsque deux corps à températures différentes sont placés à une distance arbitraire l'un de l'autre ils échangent de l'énergie par l'intermédiaire du champ électromagnétique qu'ils rayonnent dans leur environnement. Lorsque les distances de séparation sont grandes par rapport à la longueur d’onde thermique (une dizaine de microns à température ambiante), la loi de Planck (théorie du corps noir) impose une limite supérieure à ces échanges. Cette limite est donnée par la célèbre loi de Stefan-Boltzmann et correspond au flux de chaleur échangé entre deux corps noirs en interaction. Les travaux de Polder et van Hove dans les années 70 ont montré que cette limite peut être dépassée lorsque la distance est petite devant la longueur d'onde thermique (Fig. 1). A de telles distances (i.e. champ proche), le flux radiatif peut dépasser de plusieurs ordres de grandeur celui qui existe entre deux corps noirs. Cette exaltation du transfert qui résulte du transfert par effet tunnel de photons thermiques non-radiatifs est particulièrement marquée quand les corps supportent des modes de surface autour d’une longueur d’onde (tels que les phonons-polaritons dans les diélectriques et les plasmons dans les métaux) ou un continuum de modes hyperboliques.
Fig. 1. Deux corps chauds maintenus à températures T1 et T2 et séparés par un espace d’épaisseur d’échange de la chaleur à travers des photons propagatifs et non-propagatifs.
Travaux de recherche
Conversion TPV de champ proche
Le principe de la conversion TPV de champ proche a été suggéré récemment pour convertir l’énergie transportée par ce champ électromagnétique localisé en électricité à travers une cellule photovoltaïque. D’un point de vue théorique, la puissance électrique susceptible d’être généré par une cellule TPV de champ proche de 250 cm2 de section pourrait atteindre (en supposant une efficacité quantique de 100% pour la cellule photovoltaïque) 25 kW, c’est-à-dire une puissance comparable à la demande énergétique d’une habitation moyenne aux USA. Malheureusement, le décalage spectral entre l’onde de surface supportée par le corps chaud et le gap du matériau semiconducteur limite très fortement l’efficacité de ce type de cellule.
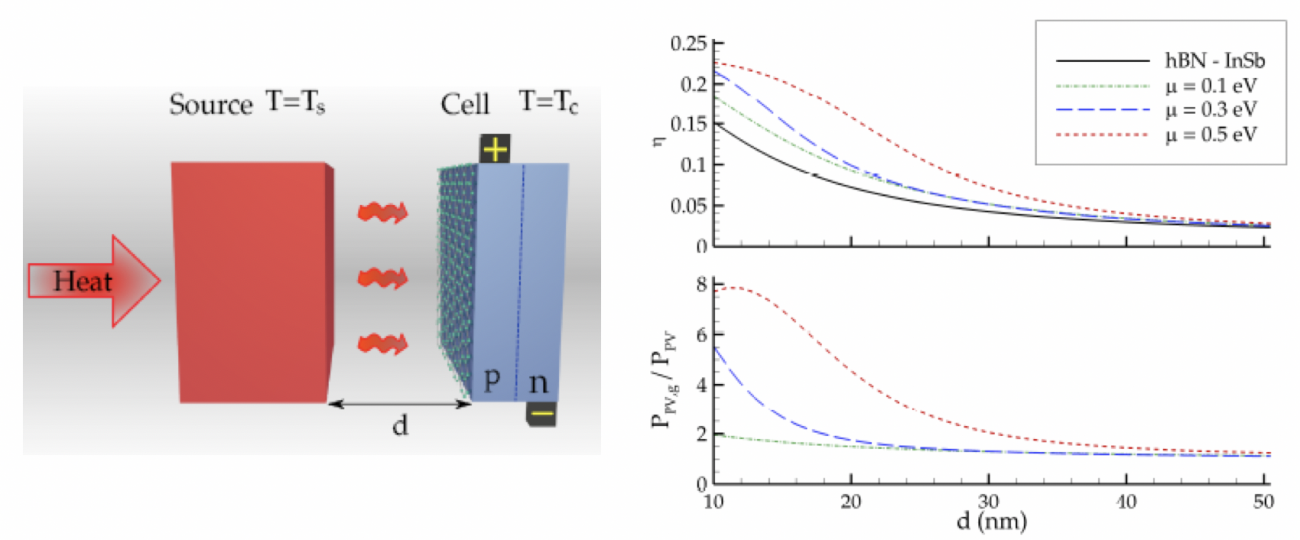
Récemment la théorie du transfert de chaleur à N-corps a été utilisée pour concevoir un nouveau type de cellule PV hybride à base de graphène. Ce type de cellule (Fig. 2) permet de s’affranchir du problème du mismatch fréquentiel entre la source chaude et la cellule PV.
Fig. 2. (A gauche) Schéma de principe d’un système de conversion TPV de champ proche à base de graphène. Une source chaude hBN (temperature Ts) est place en face d’une cellule PV en InSb recouverte de graphène et à température Tc. (A droite) efficacité et puissance électrique produite par le système avec et sans graphène. D’après Sci. Rep. 3 1383 (2013).
En outre on a mis en évidence en 2013 que le graphène [Phys. Rev. B 87, 085421, (2013)] permet de modifier activement et de façon extrêmement rapide (à l’échelle de la picoseconde) le comportement optique en champ proche de certains matériaux polaires grâce à un mécanisme de couplage fort entre le plasmon du graphène (tunable) et le phonon-polariton du matériau. Cette propriété ouvre de nombreuses perspectives pour le contrôle dynamique de l’émission sponatnnée de nano-objets placés au voisinage de ces surfaces et pour le management thermique actif à nanoéchelle.
Relaxation thermique en champ proche
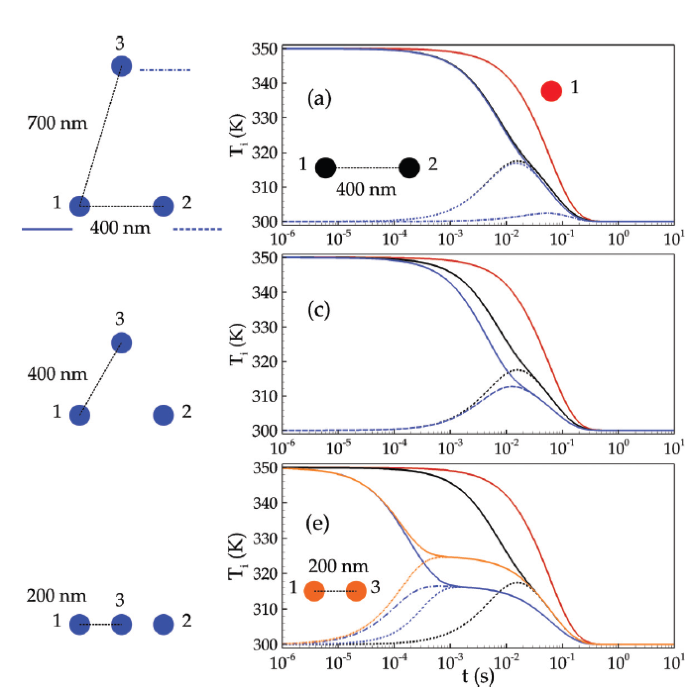
En 2013, la dynamique de relaxation de systèmes à N corps a également été étudiée [Phys. Rev. B 88, 104307 (2013)]. On a établi (Fig. 3) que cette dynamique était fortement dépendante de la position relative des objets. En outre le processus de thermalisation s’effectue généralement en deux étapes. Dans un premier temps, les particules se thermalisent entre elles par interaction de champ proche puis elle relaxe vers la température du bain environnant par échange radiatif en champ lointain.

Fig. 3. Évolution temporelle de la température de trois nanoparticules de SiC en situation de hors équilibre vs leur position [d’après Phys. Rev. B 88, 104307 (2013)]. En rouge, dynamique de relaxation d’une particule isolée et d’une paire de particules.
Thermotronique : vers le développement de circuits pour le contrôle des flux de chaleur
La diode et le transistor constituent les éléments clés en électronique et dans les technologies de l’information qui ont révolutionné notre vie de tous les jours. Grace à ces capacités de contrôle (modulation, commutation, amplification) des courants électriques, le transistor constitue la brique élémentaire pour concevoir des portes logiques, des mémoires etc….
Une part importante de mes travaux ces dernières années a été consacrée au développement d’analogue thermique de ces briques de base en vue de contrôler les flux de chaleur échangés par rayonnement (en champ proche et en champ lointain) entre des objets à la manière du flux d’électron dans les circuits électriques.
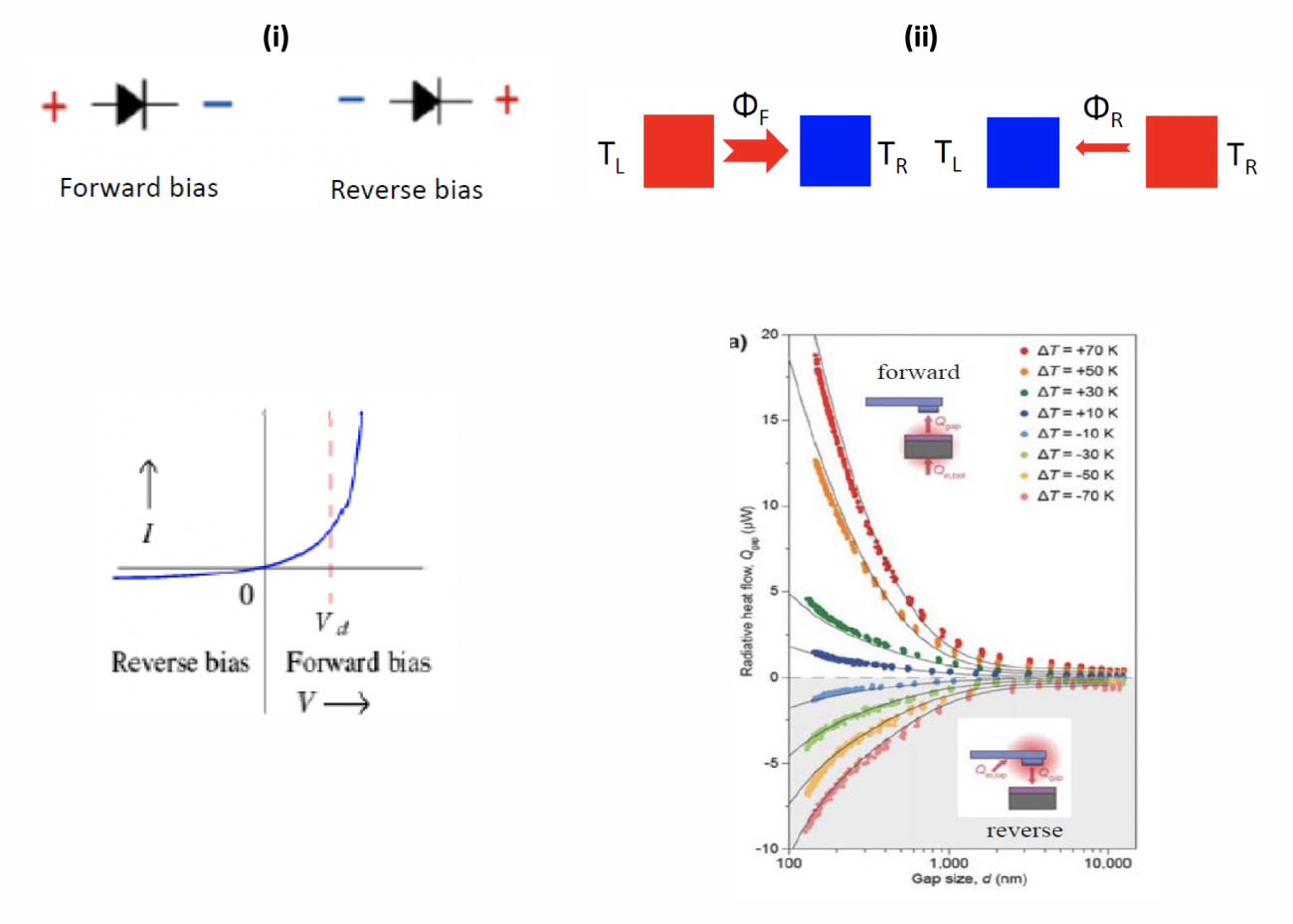
Fig. 4. (a)- Diode électrique (i) et thermique (ii). De façon analogue à la diode électrique qui laisse passer le courant électrique dans un sens (forward bias), tout en le bloquant dans l'autre (reverse bias) la diode thermique autorise le transfert de chaleur dans un sens (forward scenario) et tend à s’opposer au transfert dans l’autre sens lorsque le gradient de température est inversé.
En 2014, après avoir développé une diode thermique à base de matériaux à changement de phase (cette prédiction théorique a été vérifiée expérimentalement en 2018, [cf. Fig. 4(a) et ACS Nano 12, 5774 (2018)], nous avons introduit un analogue thermique du transistor [Phys. Rev. Lett. 112, 044301 (2014)].

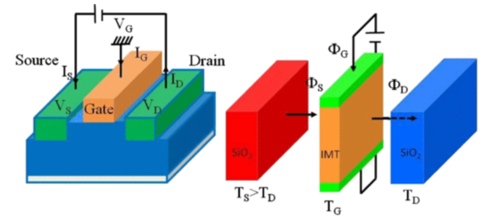
Fig. 5. Principe du transistor thermique radiatif. (A gauche) Transistor à effet de champ classique: composé par trois éléments de base la source, la grille et le drain. La grille est utilisée pour contrôler activement le flux d’électrons échangé entre la source et le drain en appliquant une différence de potentiel sur la grille de façon à modifier la conductivité électrique apparente entre la source et le drain. (A droite) transistor thermique radiatif : composé d’une couche de matériau à transition métal-isolant placée entre deux réservoirs de températures  et
et  avec
avec  . En changeant la température
. En changeant la température  de la grille on change les propriétés optiques de celle-ci et par voie de conséquence le flux
de la grille on change les propriétés optiques de celle-ci et par voie de conséquence le flux  reçu par le drain et le flux
reçu par le drain et le flux  perdu par la source. Lorsque la température de la grille est légèrement plus petite que la température critique (i.e. température de transition) Tc une légère augmentation de la température induit une forte variation des flux
perdu par la source. Lorsque la température de la grille est légèrement plus petite que la température critique (i.e. température de transition) Tc une légère augmentation de la température induit une forte variation des flux  et
et  . Le transistor fonctionne alors en mode « on-off ». Au voisinage de la transition une diminution de la température de la grille induit une forte augmentation du flux reçu par le drain. Ce comportement reflète la résistance différentielle négative de la grille au voisinage de Tc et induit une amplification du flux reçu par le drain (c’est « l’effet transistor ») [d’après P. Ben-Abdallah and S.-A. Biehs, Phys. Rev. Lett. 112, 044301 (2014)].
. Le transistor fonctionne alors en mode « on-off ». Au voisinage de la transition une diminution de la température de la grille induit une forte augmentation du flux reçu par le drain. Ce comportement reflète la résistance différentielle négative de la grille au voisinage de Tc et induit une amplification du flux reçu par le drain (c’est « l’effet transistor ») [d’après P. Ben-Abdallah and S.-A. Biehs, Phys. Rev. Lett. 112, 044301 (2014)].
Le principe de fonctionnement de ce transistor consiste (Fig. 5) à la manière du transistor à effet de champ à contrôler le flux échangé entre le milieu chaud (la source) et le milieu froid (le drain) à l’aide d’un slab intermédiaire (l’analogue de la grille) dont les propriétés optiques peuvent être pilotées par une action extérieure.
Fin 2014 nous avons mis en évidence, l’existence possible de plusieurs états d’équilibre thermique dans les systèmes à n-corps. Le comportement bistable de ces systèmes a permis de concevoir une mémoire thermique (Fig. 6(a)) capable de stocker de la chaleur pendant une durée arbitrairement longue et de la relâcher dans son environnement à la demande [Phys. Rev. Lett. 113, 074301 (2014) et PRL Focus]. Ces résultats ouvrent la voie à une nouvelle technologie baptisée ‘thermotronique’ pour le management thermique sans contact à macro et nanoéchelle [AIP Advances 5, 053502 (2015)].

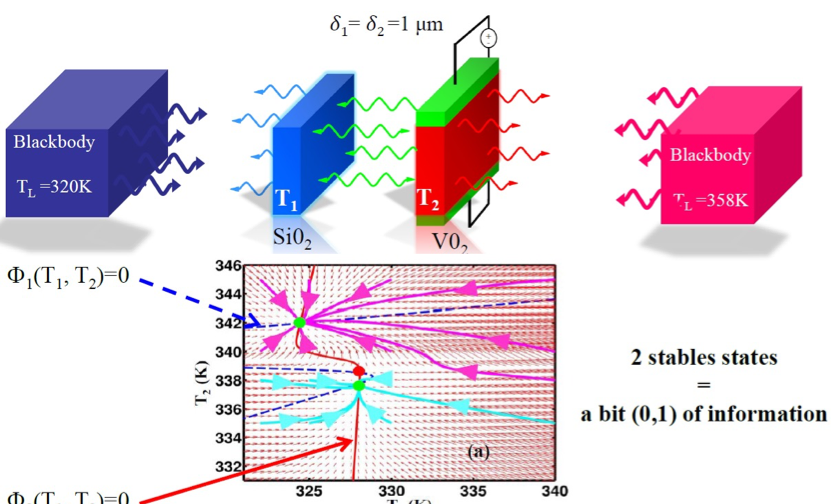
Fig. 6. (a) Principe d’une mémoire thermique radiative volatile. Deux membranes qui échangent de la chaleur par rayonnement et sont en interactions avec deux bains thermiques (champ rayonné par deux corps noirs externes) peuvent posséder plusieurs températures d’équilibre lorsqu’on moins une des membranes est composée d’oxide de vanadium, un matériau à transition de phase métal-isolant. En changeant la phase de ce matériau à l’aide d’un réseau d’électrodes et d’éléments Peltier, il est possible de commuter d’un état d’équilibre (état « 0 ») vers l’autre «(état « 1 »). Ces deux états d’équilibre constituent un bit thermique. Tant que le bain thermique externe est maintenu, la mémoire demeure stable.
Enfin, en 2016 nous avons conçu les toutes premières portes logiques [Phys. Rev. B 94, 241401(R) (2016)] pour un traitement radiatif de l’information. Nous avons montré qu’en combinant en série ou en parallèle des matériaux à changement de phase des portes NOT, OR et AND peuvent être réalisés (Fig. 7(b)).
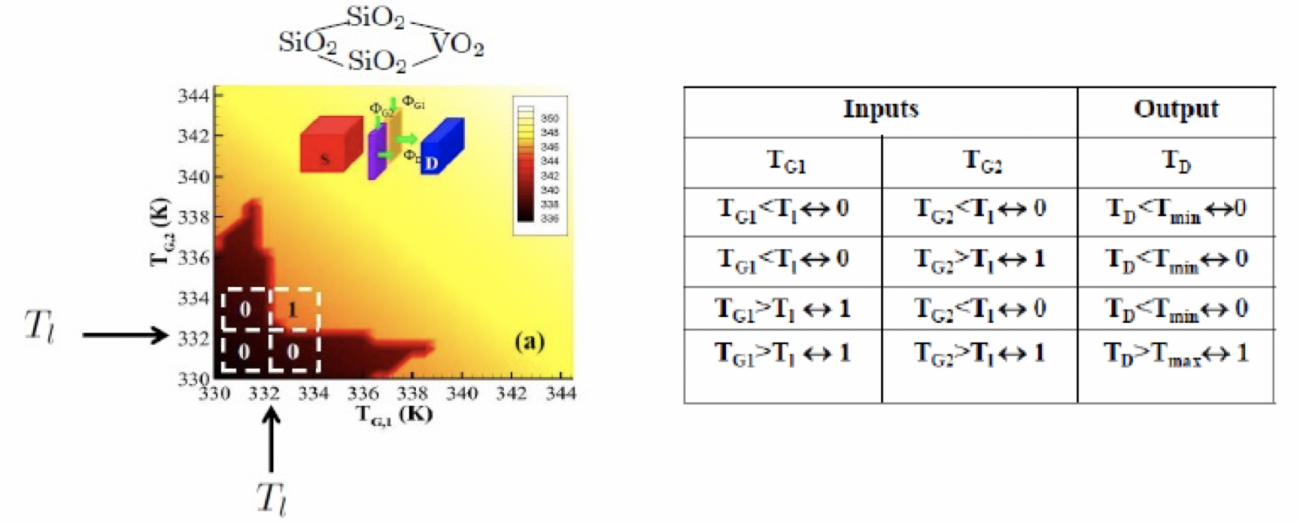
Fig. 7-b-Porte AND constituée d’un transitor thermique à double porte (G1, G2) de 250 nm d’épaisseur en SiO2 . La source (S) semi-infinie est en SiO2 tandis que le drain (D) est consitué d’un matériau à changement de phase (VO2) de 500 nm d’épaisseur. La distance de séparation entre les différents éléments est d = 100 nm et les portes sont supposées isolées l’une de l’autre. Le graphe (à gauche) représente la température TD du drain en fonction des températures TG1 et TG2 des deux portes. Le domaine de fonctionnement de la porte logique est délimité par le domaine rectangulaire en pointillé centré à (TG1, TG2) = (Tl, Tl) avec Tl = 332.2 K. A droite est représentée la table de vérité de la porte AND.
Transfert de chaleur dans les systèmes à N corps.
Depuis les années 70 et jusqu’au début des années 2000 seul les échanges chaleur entre deux objets ont été étudié. Or, le caractère non-additif des transferts radiatifs suggère une physique différente lorsque plusieurs corps interagissent. En 2011 nous avons étendu la théorie des transferts de chaleur en champ proche aux systèmes à N-corps en interaction [Phys. Rev. Lett. 107, 114301 (2011)]. Dans ces systèmes, les fluctuations thermiques locales génèrent des oscillations de charges dans chaque objet qui, par voie de conséquence, rayonne dans leur environnement. Les champs ainsi produits interagissent avec les différents objets en interaction et génèrent à leur tour des champs secondaire et ainsi de suite (Fig. 8). Ce type de problème appartient à la catégorie des problèmes à N-corps que l’on retrouve dans de nombreux domaines de la physique (physique de la matière condensée, physique atomique, chimie quantique, mécanique céleste…).
Fig. 8. Coefficient d’échange en champ proche entre deux nanoparticules de SiC à température T1=300K et T2= 0K en présence d’une troisième particule de SiC à température nulle. Le coefficient d’échange est normalisé par le coefficient d’échange entre deux particules isolées. D’après Phys. Rev. Lett. 107, 114301 (2011).
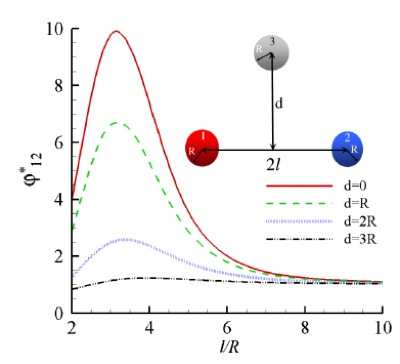
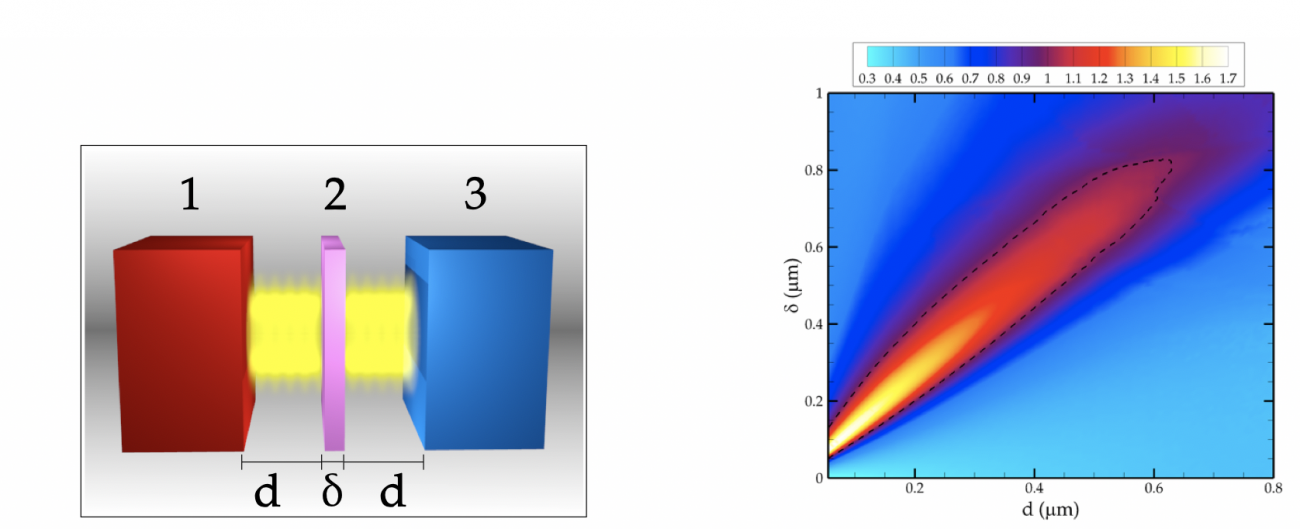
Parallèlement à cela, un effet d’amplification à trois corps (Fig. 9) a été mis en évidence. Cet effet est lié à la présence d’un matériau dit relais intercalé entre deux milieux en interaction. Le relais a pour effet de compenser, grâce à un mécanisme d’interaction à trois corps, et de façon totalement passive (aucun apport externe d’énergie n’est nécessaire) la décroissance exponentielle du flux échangé en champ proche entre deux objets. Ainsi, il devient désormais possible d’exporter des effets de champ proche à plus grandes distances qu’habituellement.


Fig.9 : Amplification du transfert de chaleur dans un système à trois corps. A droite, le taux d’amplification [d’après R. Messina, M. Antezza, and P. Ben-Abdallah, Phys. Rev. Lett. 109, 244302 (2012)].
Thermo-magnétoplasmonique :
Récemment un nouveau champ de recherche a été développé. Il concerne les transferts de chaleur dans les structures plasmoniques complexes soumises à un champ magnétique externe. Un nouvel effet Hall thermique a été mis en évidence [Phys. Rev. Lett. 116, 084301 (2016)]. L’effet Hall classique découvert par Edwin Hall à la fin du 19e siècle consiste en l’apparition d’un courant électrique transverse dans un conducteur sous l’action d’un champ magnétique externe appliqué dans une direction orthogonale au gradient de tension. Cet effet est dû à la force de Lorentz qui agit transversalement sur les charges électriques en mouvement à travers le champ magnétique, incurvant ainsi leurs trajectoires. Très peu de temps après cette découverte un analogue thermique de cet effet a été observé par Righi et Leduc lorsqu’un gradient de température est appliqué à travers un conducteur électrique. Comme pour l’effet Hall classique, c’est la présence de charges électrique dans un champ magnétique qui est à l’origine de l’apparition d’un flux de chaleur transverse. Ainsi, on pourrait s’attendre à ce qu’aucun effet Hall thermique n’existe en l’absence de charges libres.


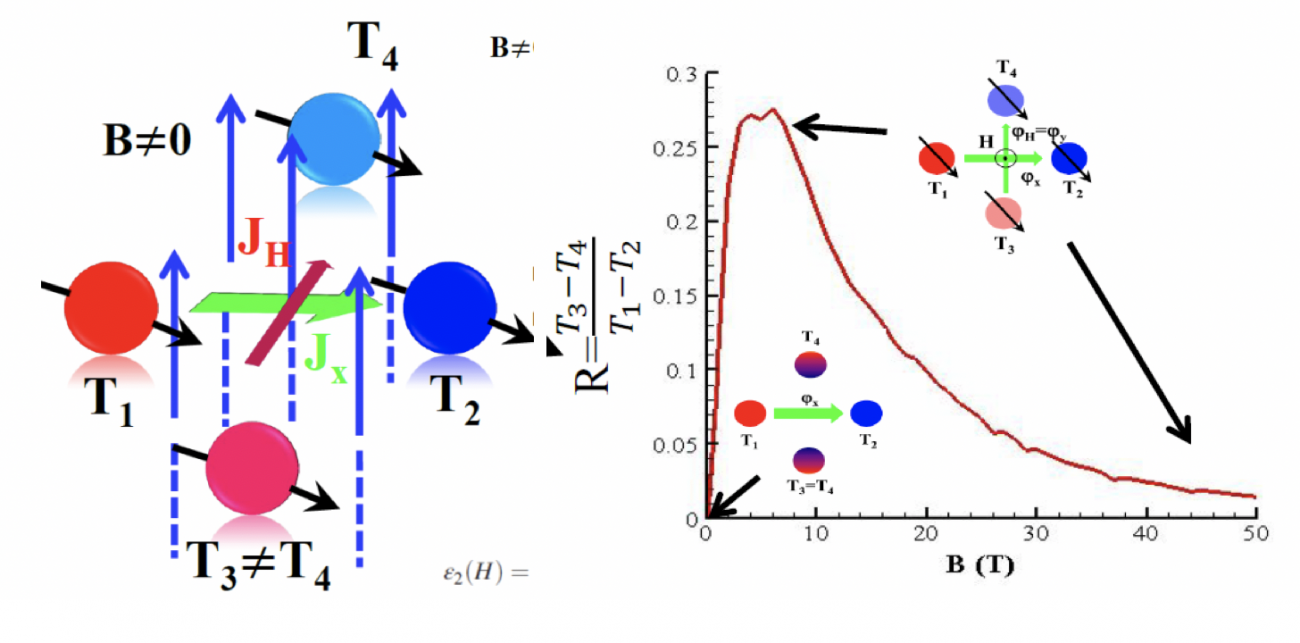
Fig. 10. (a) A gauche, système composé de 4 nanoparticules magnéto-optiques (InSb) placées aux sommets d’un carré et soumises à un champ magnétique B perpendiculairement au carré. A droite, température de Hall normalisée par la différence de température entre les particules 1 et 2. Le champ magnétique brise la symétrie du système et génére un flux de chaleur perpendiculaire au flux primaire entre les particules 1 et 2 [d’après Phys. Rev. Lett. 116, 084301 (2016)].
Pourtant, durant la dernière décennie, différentes équipes de recherche ont mis en évidence la présence de cet effet dans des matériaux isolants et établis que l’apparition d’un flux de chaleur transverse pouvait être dû à un comportement anormal des phonons ou des magnons (ondes de spin). Or, on a récemment prédit [Phys. Rev. Lett. 116, 084301 (2016)] que les photons peuvent aussi être à l’origine d’un effet Hall thermique dans des réseaux de particules magnéto-optiques (Fig. 10(a)). Ce résultat ouvre de nouvelles perspectives de recherche dans le domaine du management thermique grâce au contrôle actif des mécanismes d’interaction coopératifs dans des structures magnéto-plasmoniques.
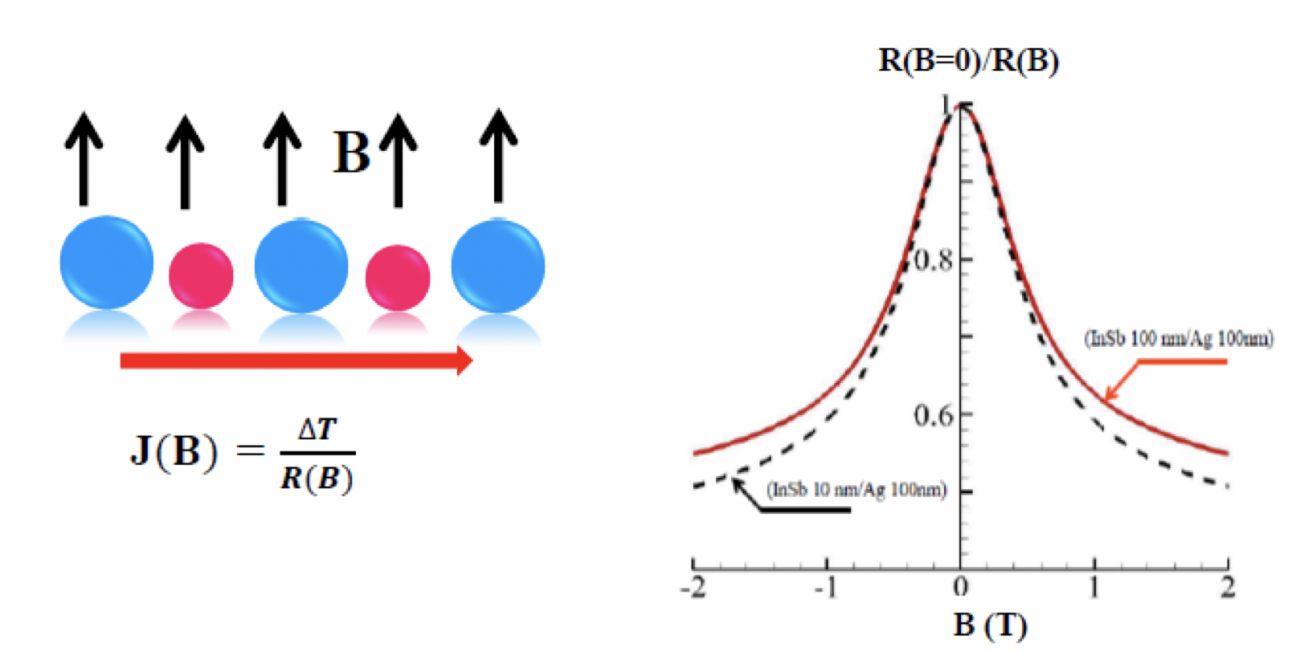
Fig. 11 (b) Magnétoresistance thermique à T=300K de chaines binaires de nanoparticules InSb-Ag en fonction de l’intensité B du champ magnétique appliqué orthogonalement à l’axe de la chaine. Le rayon des nanoparticules vaut r = 100 nm tandis que la distance entre deux particules adjacentes (bord à bord) est d=2r.
Récemment nous avons mis en évidence [Phys. Rev. Lett. 118, 173902 (2017)] un nouvel effet thermomagnétique dans les réseaux de nanoparticules magnéto-optiques : une résistance thermique magnétique géante (Fig. 11). Cette résistance résulte du fort décalage spectral des modes de surface localisés supportés par les particules sous l’action d’un champ magnétique de faible intensité. Cet effet, qui existe à température ambiante, pourrait être mis à profit pour contrôler activement les transferts de chaleur en champ proche et pour détecter la présence de champ magnétique à partir de simples mesures de température.
Regimes de transport anormaux dans les systèmes à N-corps
A – Superdiffusion de la chaleur dans les réseaux de nanostructures plasmoniques
Il est communément admis depuis les travaux de Joseph Fourier au 19ème siècle que la chaleur se propage dans les solides en suivant un processus de diffusion dit normal. Du point de vu microscopique, les porteurs de chaleur (phonons ou électrons) se déplacent à travers le réseau atomique des matériaux en suivant un processus de marche au hasard Gaussien. La vitesse de propagation de la chaleur au sein du solide est alors définie par la vitesse de déplacement des porteurs et par la distance que ces derniers sont capables de couvrir entre deux collisions.
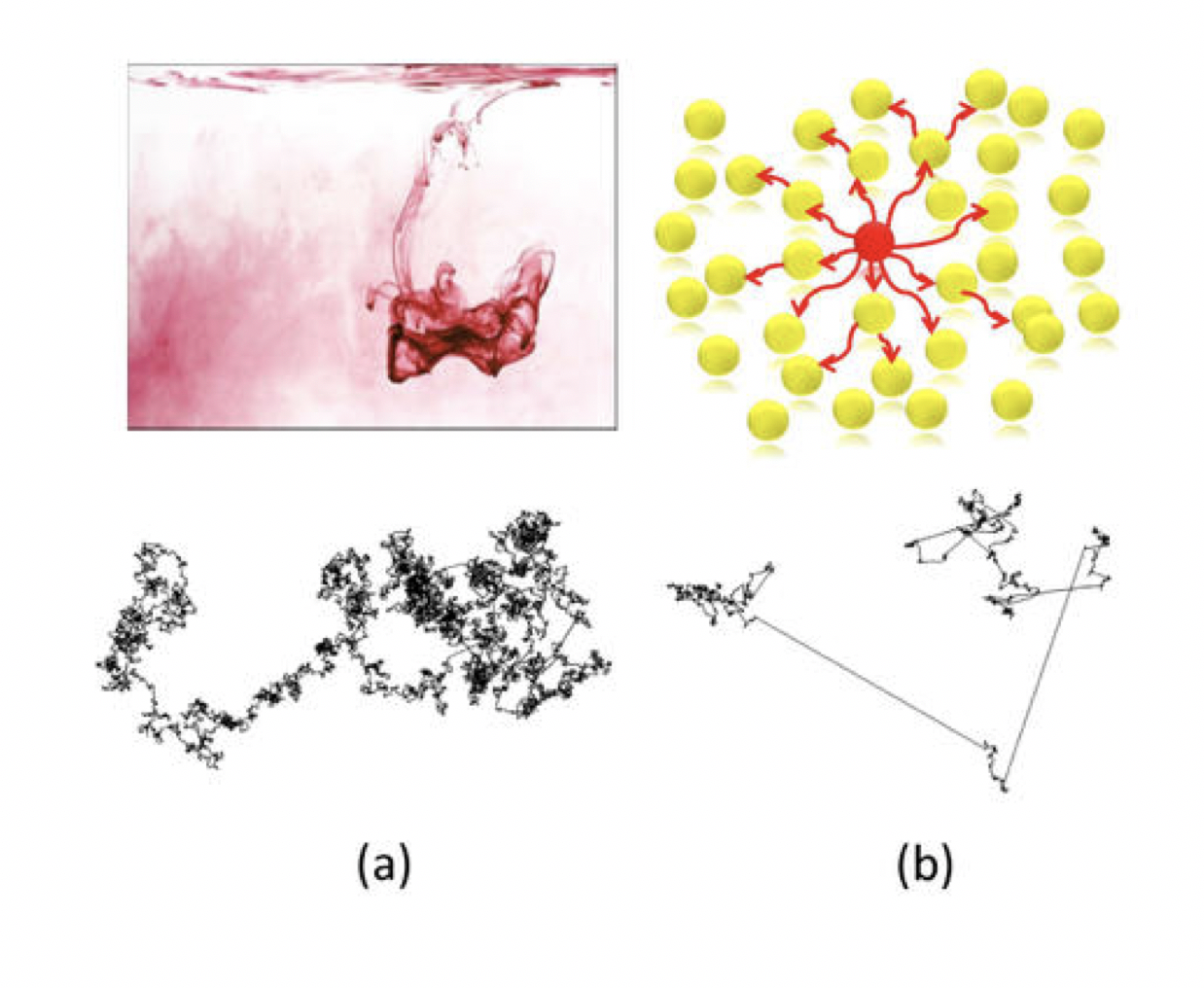
Dans ce travail (cf. Fig. 12(a)), nous avons établi [Phys. Rev. Lett. 111, 174301, (2013)] que lorsque l’on insert un réseau de nanoparticules plasmoniques (i.e. nanoparticules qui supportent des modes électromagnétiques localisés), la chaleur peut se propager plus rapidement que dans un solide ordinaire. Ce mécanisme de transport « superdiffusif » est relié aux interactions de champ proche entre les nanoparticules (effets collectifs) au sein du réseau qui se comporte alors comme un super-canal pour le transport de la chaleur.
Ce résultat ouvre la voie à de nombreuses opportunités en science des matériaux en particulier pour la conception de matériaux innovants pour le management thermique à haute fréquence.
Fig. 12. (a) Superdiffusion de la chaleur dans des réseaux de structures plasmoniques. A gauche, diffusion d'un colorant dans de l'eau. Les particules de colorant suivent une marche au hasard qui obéit à un processus de diffusion Gaussien (a). A droite, propagation de la chaleur par interaction de champ proche dans un réseau de nanoparticules plasmoniques. La chaleur se propage à travers le réseau en suivant un processus de Lévy (b).
B – Transport ballistique de la chaleur dans les systèmes à N-corps denses
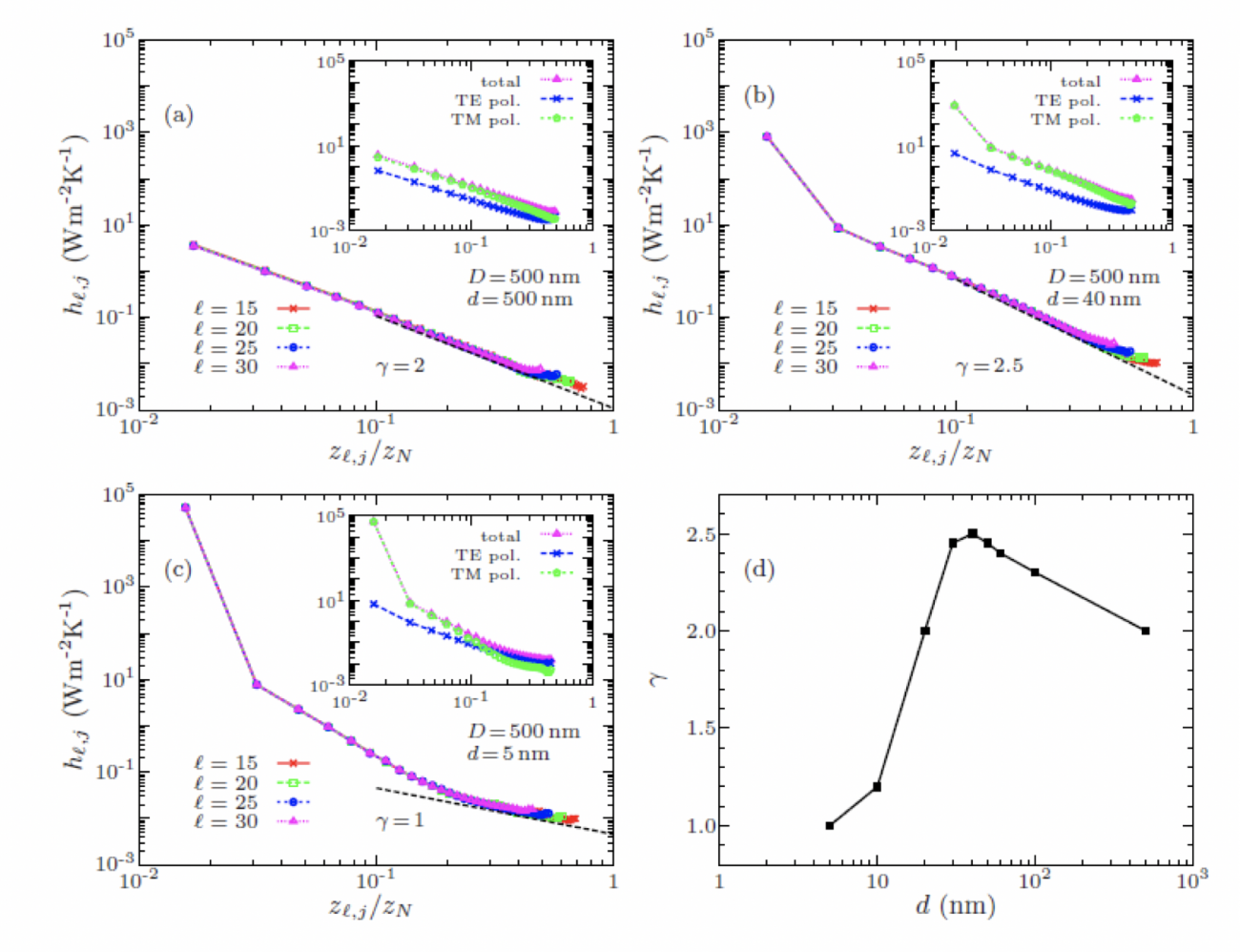
Comme nous venons de le voir, dans les milieux dilués le régime de transport en champ proche dans les systèmes à N corps est superdiffusif. En 2017 nous avons montré à l’aide d’une théorie de Landauer généralisé que nous avons développé [Phys. Rev. B 95, 205404 (2017)] que dans les systèmes denses le régime de transport devient ballistique. Ce régime de transport change radicalement la dynamique de relaxation dans les systems à N-corps en réduisant de plusieurs ordres de grandeurs le temps de relaxation (Fig. 13).
Fig. 13. Coefficient de transfert entre deux films de SiC en fonction de leur distance de séparation dans un réseau de 60 films séparés de (a) d = 500 nm, (b) d = 40nm et (c) d = 5 nm. Les courbes en pointillé indiquent le comportement asymptotique de h en 1/zg . La valeur de g indique la nature du régime de transport depuis le régime superdiffusif (1 < g< 3) au régime ballistique (g® 1). Les inserts représentent la contribution des deux états de polarization TE et TM au coefficient d’échange. (d) Exposant g en fonction de la distance de séparation d entre les films.
Shuttling radiatif
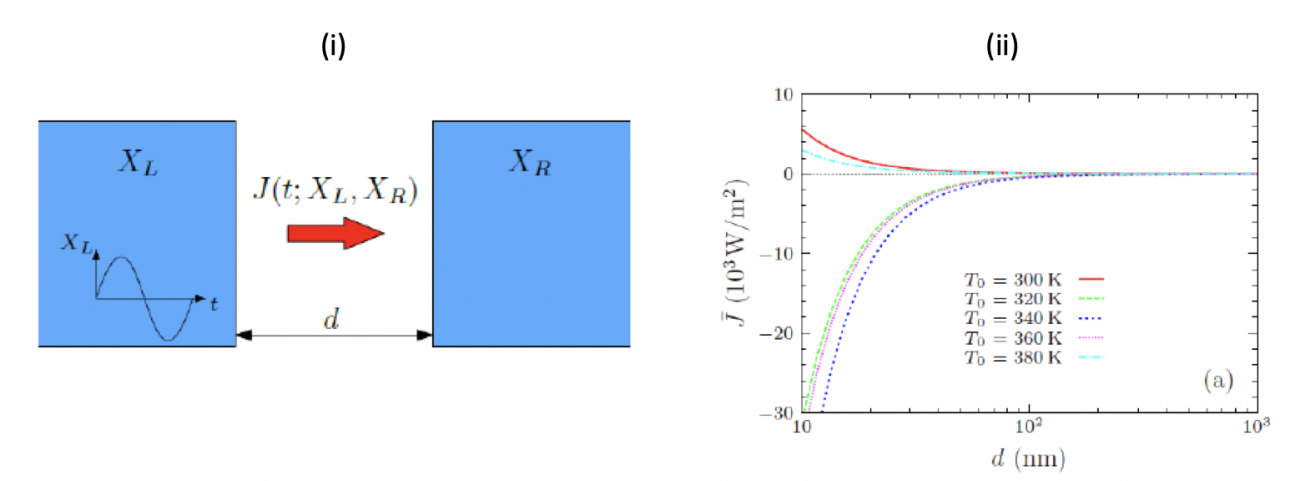
En 2018 nous nous sommes intéressés aux échanges de chaleur en champ proche entre deux objets lorsque leur température où leur potentiel chimique est modulé dans le temps à une échelle plus grande que le temps de relaxation thermique de ces objets. Nous avons mis en évidence la présence d’un nouveau mécanisme [Phys. Rev. Lett. 121, 023903 (2018)] appelé « shuttling radiatif » qui se superpose au transfert de chaleur moyen et qui peu amplifié ou inhiber ce dernier selon le signe de la résistance thermique différentielle (Fig. 14) qui sépare les deux objets. Cet effet pourrait jouer un rôle important dans le développement des systèmes électromécaniques à nanoéchelle où les fluctuations de température sont importantes (celles-ci augmentent à mesure que la taille des objets diminue) et plus généralement dans de domaine du management thermique.
Fig. 14 Flux de chaleur moyen échangé entre un film de VO2 (L) et un film de verre (R) lorsque la température du VO2 est modulée de façon sinusoidale (ie. TL(t)=T0+dT sin(Wt)) avec une amplitude dT=30 K tandis que TR est maintenue à temperature constante T0 (la fréquence de modulation est supposée petite devant l’inverse du temps de thermalisation).
Moteurs thermiques en champ proche
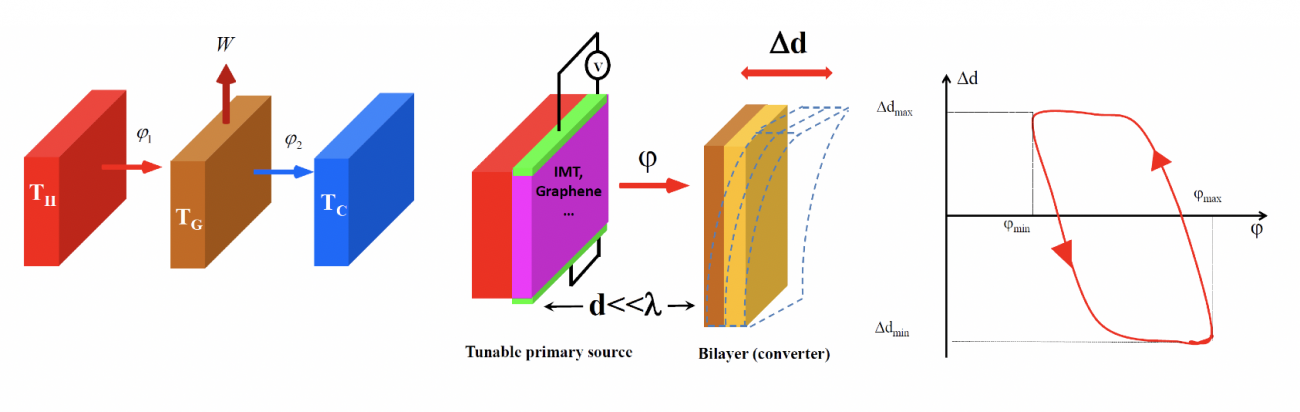
Un moteur thermique est un système qui converti une partie du flux de chaleur produit par une source chaude en travail mécanique à l’aide d’un convertisseur. Ce dernier transfert une partie de sa chaleur vers une source froide. Pour des systèmes hors contact qui sont séparés par de grandes distances la puissance maximale qui peut être transférée au convertisseur est limité par la loi de Stefan Boltzmann (limite du corps noir). A courte distance de séparation, la participation du champ électromagnétique évanescent permet d’aller bien au-delà de cette limite. Jusqu’à présent, la conversion thermophotovoltaique de champ proche est le seul principe qui a été proposé pour extraire l’énergie thermique de champ proche. En 2015 les principes de base d’un système de conversion de l’énergie de champ proche a été étudié. L’idée décrite sur la Fig. 15 est la suivante. Une membrane oscillante est placée entre un corps chaud et un corps froid (qui font office de réservoir) à une distance sub-longueur d’onde de chacun d’eux. Le flux de chaleur, transféré entre les deux réservoirs via la membrane est modulé (par transition de phase ou à l’aide d’un feuillet de graphène qui est dynamiquement dopé) de sorte que le flux reçu par la membrane oscille. Cette oscillation engendre une dilatation thermique de la membrane et l’hystérésis de son champ de déplacement.
Fig. 15. (A gauche) Principe général d’une moteur thermique sans contact. Une source primaire de température TH rayonnement en direction d’un système qui converti une partie de ce flux incident en travail mécanique. L’énergie résiduelle est transférée vers une source froide à température TC < TH. (A droite) Le couplage en champ proche entre un corps chaud et une membrane bistable permet de générer une oscillation (hystérésis du déplacement) de la membrane en modulant le flux émit par le corps chaud.
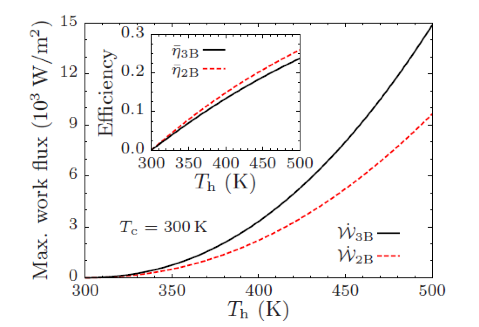
Avant de s’attaquer au problème du couplage entre l’oscillateur mécanique et les deux réservoirs nous avons étudié [Phys. Rev. Applied 4, 011001 (2015)] les performances thermodynamiques (Fig. 16) de ce type de nanomoteur.
Fig. 16. Puissance maximale que l’on peut extraire d’un système de conversion à 3 corps (3B) en champ proche comparé à celle que l’on peut extraire d’un système à 2 corps (2B). L’insert montre les efficacités de conversion. [d’après Phys. Rev. Applied 4, 011001 (2015)].
Selection de publications
[1] A. Ott, R. Messina, P. Ben-Abdallah, and S.-A. Biehs, Magnetothermoplasmonics: from theory to applications, J. Photon. Energy 9, 032711 (2019).
[2] I. Latella, R. Messina, J. M. Rubi, and P. Ben-Abdallah, Radiative heat shuttling, Phys. Rev. Lett. 121, 023903 (2018).
[3] A. Fiorino, D. Thompson, L. Zhu, R. Mittapally, S.-A. Biehs, O. Bezencenet, N. El-Bondry, S. Bansropun, P. Ben-Abdallah, E. Meyhofer, P. Reddy, A thermal diode based on nanoscale thermal radiation, ACS Nano 12, 5774 (2018).
[4] R. Messina, S.-A. Biehs, and P. Ben-Abdallah, Surface-mode-assisted amplification of radiative heat transfer between nanoparticles, Physical Review B 97, 165437 (2018).
[5] P. Ben-Abdallah, Photon thermal Hall effect, Phys. Rev. Lett. 116, 084301 (2016).
[6] P. Ben-Abdallah and S.-A. Biehs, Near-field thermal transistor, Phys. Rev. Lett. 112, 044301 (2014).
[7] R Messina and P. Ben-Abdallah, Graphene-based photovoltaic cells for near-field thermal energy conversion, Sci. Rep. 3, 1383 (2013).
[8] S.-A. Biehs, M. Tschikin, R. Messina, and P. Ben-Abdallah, Super-Planckian near-field thermal emission with phonon-polaritonic hyperbolic metamaterials, Appl. Phys. Lett. 102, 131106 (2013).
[9] R. Messina, M. Tschikin, S.-A. Biehs, P Ben-Abdallah, Fluctuation-electrodynamic theory and dynamics of heat transfer in systems of multiple dipoles, Phys. Rev. B 88, 104307 (2013).
[10] R. Messina, M. Antezza, and P. Ben-Abdallah, Three-body amplification of photon heat tunneling, Phys. Rev. Lett. 109, 244302 (2012).